Calculs justificatifs de faisabilité

La démonstration de faisabilité du velum imaginé passe nécessairement par le dimensionnement des câbles et des efforts à mettre en œuvre. Prouver que des cordes en chanvre de diamètres raisonnables conviennent et que l'installation et les manœuvres du velum ne nécessitent que des efforts modérés est donc l'objectif des pages de cet onglet.

Methode imaginée

Il a été choisi de calculer le velum d'allure elliptique d'un amphithéâtre antique par extrapolation des calculs appliqués à un amphithéâtre circulaire virtuel ayant un rayon de même valeur que le plus grand rayon de courbure du dit amphithéâtre et avec un nombre de mâts procurant une distance de l'un à l'autre très proche de celle mesurée sur les supports sauvegardés (3m à Nîmes, 2m au Colisée). C'est en effet au droit de ce plus grand rayon de courbure que les tensions centripètes des bras et des drisses engendrent les plus importantes réactions tangentielles sur l'anneau central.

La méthode consiste a déterminer d'abord les efforts aux extrémités d'un filin d'assemblage de deux rectangles élémentaires de toile puis à reporter ceux-la en sens inverse sur les autres organes avec lesquels il est en contact (action = réaction) et ainsi de suite. L'équilibre est acquis quand simultanément sont nulles la somme algébrique des efforts en X, la somme algébrique des efforts en Y, la somme algébrique des moments des forces par rapport à un point quelconque.

La mise en équations des efforts concerne un sous ensemble constitué :

• --- d'un bras (en marron)
• --- d'un rectangle élémentaire de toile (en rouge)
• --- d'un filin de réunion de deux rectangles de toile voisins
• --- de la quote-part d'anneau central associée au rectangle de toile
• --- d'une drisse de déploiement, repliement
• --- d'un ensemble poulie de drisse.

Conventions Particulières

Les efforts seront représentés par leurs projections sur les habituels axes orthogonaux X et Y, orientées dans leurs sens réels, ici détectables sans aucune ambiguïté car les tensions exercées à chaque extrémité d'un filin souple ne peuvent qu'être de même direction que les tangentes à celles-la. Cette disposition permet de ne porter dans les équations que les valeurs absolues des forces en jeu. Il ne restera qu'à bien doter d'un certain signe les moments provoquant tel sens de rotation et d'un signe opposé ceux provoquant un sens de rotation contraire.

Entorse aux bonnes règles ? pour simplifier les écritures il a été choisi d'opérer avec le système d'unités MKpS, celui la permettant d'exprimer les poids avec les mêmes valeurs que les masses qui les engendrent. Dans cet ancien système une masse d'un kilogramme pèse un kilogramme force tandis qu'elle pèse 9,81 newton dans le système légal d'aujourd'hui…

Le moment par rapport à un point du poids uniformément réparti de la toile ou d'un câble étant de même valeur que celui de la résultante sera exprimé avec la dite résultante. Les longueurs de la toile et des câbles seront considérées comme étant celles des droites joignant leurs deux extrémités au motif que la différence est faible (3% pour une flèche de 10% de la longueur de «chaînette»).

Données Géometriques

Selon l'ouvrage de Jean Claude Golvin et Christian Landes « Amphithéâtres et gladiateurs » (1990 aux Presses du CNRS) les périmètres des amphithéâtres antiques étaient le plus souvent obtenus par quatre arcs de cercle dont les centres sont les sommets d'un losange construit avec 4 triangles rectangle de Pythagore accolés. Dans les calculs qui suivent les amphithéâtres seront considérés avec des périmètres extérieurs définis selon cette règle.

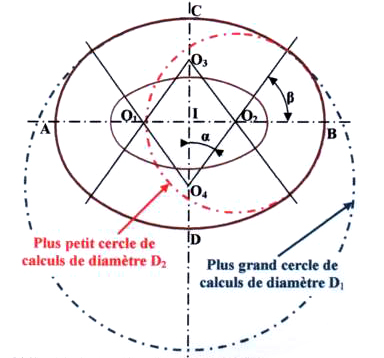En désignant par u une longueur de module de base de construction de l'amphithéâtre on a : I O1 = 3.u ; I O3 = 4.u ; O1 O3 = 5.u A et B étant la longueur et la largeur de l'amphithéâtre on a : (1) A = D2 + 6u (2) B = D1- 8u (3) D1/2 – D2/2 = 5u Les 3 équations (1), (2) et (3) permettent de calculer D1 et D2 à partir de la longueur A et de la largeur B de l'amphithéâtre D1= 2.A – B et D2 = (3.B - A)/2 Les angles de construction α et β en radian sont : α = arc sin(3/5) et β = arc sin(4/5)

Ainsi qu'écrit précédemment les calculs se font pour des velums circulaires virtuels ayant des rayons de même valeur que celui des arcs de grands rayons de l'amphithéâtre concerné… et avec des nombres de mâts N₁ et N₂ procurant des écartements très proches de celui que l'on peut encore mesurer sur les ruines (2,25m pour le Colisée, 3,10 m pour les arènes de Nîmes). Cette disposition fait que les velums virtuels pour calcul seront constitués avec des rectangles élémentaires de toile de mêmes dimensions que le rectangle élémentaire du velum d'allure elliptique à N mâts.

Le périmètre de l'amphithéâtre est donc Pe = 2. α .D₁ + 2. β. D₂

L'écartement entre mâts est l_m = Pe/N

Les périmètres du grand et du petit cercle de calcul sont :
Pe1 = 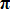.D₁ et Pe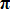2 = .D₂

Le nombre de mâts du grand cercle de calcul doit donc être N₁ tel que
Pe /N = 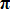.D₁/N₁ d'où N₁ = N. 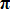.D₁/ Pe

Le nombre de mâts du petit cercle de calcul doit donc être N₂ tel que
Pe /N = 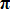.D₂/N₂ d'où N₂ = N. 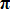.D₂/ Pe

Les valeurs données par les calculs seront arrondies à des nombres entiers pairs.

Le Colisée mesure 188 x 156 m et est équipé de 240 mâts. Pour tenir compte que son velum est accroché sur le bord d'une plateforme de 10 m de largeur on retiendra pour celui-ci un grand axe de 168 m (188 – 2.10) et un petit axe de 136 m (156- 2.10), des diamètres de cercles de calculs D₁ = 200 m et D₂ = 120 m, des nombres de mâts N₁= 314 et N₂= 188

Les arènes de Nîmes mesurent 134 x 101 m et sont équipées de 120 mâts.

D'où :

D1 = 167 m

D2 = 85 m

N1 = 170

N2 = 86

Si L est la projection de la largeur du velum de couverture la surface couverte est : Sc = 2.L.(α.D₁ + β. D₂) –2.L².(α + β)

Définition des principaux symboles utilisés

D₁ : diamètre en m du grand cercle de calculs.
D₂ : diamètre en m du petit cercle de calculs.
N₁ : nombre de mâts virtuels sur D₁
N₂ : nombre de mâts virtuels sur D₂
m_t : masse unitaire de la toile en Kg/m²
L : longueur en projection d'un rectangle élémentaire de toile
a : distance en m entre extrémités de toile et sommet d'anneau central en surplomb sur arène
p : pente au point bas du filin inséré dans la toile.
H_f : dénivelé en m du filin inséré dans la toile.
h_d : Distance en m entre haut de filin dans toile et brin supérieur de drisse.
h_br : Distance en m entre haut de filin dans toile et bras.
R : résistance à la rupture en Kg/mm² de l'ensemble des câbles utilisés.
d : densité en Kg/dcm³ de l'ensemble des câbles utilisés.
K_f : coefficient de sécurité à la rupture souhaité pour le filin inséré dans la toile.
K_a :coefficient de sécurité à la rupture souhaité pour le câble d'anneau central.
m_p : masse en Kg d'un ensemble poulie de drisse
z : Rapport des diamètres de câble de drisse et du filin inséré dans la toile.
y : Rapport des diamètres du câble de bras et du câble de drisse.
l₊ : supplément en m de largeur de rectangle de toile, pour assemblage.
N : Nombre de mâts de l'amphithéâtre.
E : module d'élasticité du bois des mâts.
R_m : Résistance à la rupture du bois des mâts en Kgf/mm².
K_m : Coefficient de sécurité à la rupture souhaité pour les mâts.
ø_tr : Diamètre du treuil en mm
L': longueur en projection de la drisse et du bras : L' = L + a
L_t : longueur approchée d'un rectangle de toile, en m.
L_d : longueur approchée du brin supérieur de la drisse, en m.
L_b : longueur approchée d'un bras, en m.
l_m1 : distance en m entre deux mâts du velum virtuel de diamètre D₁.
l_m2 : distance en m entre deux mâts du velum virtuel de diamètre D₂.
l_t : largeur en m d'un rectangle de toile du velum. On convient que l_t = l_m1 + l₊
H_d : dénivelé en m du brin supérieur de drisse = H_f + h_d
m_f : masse unitaire du filin inséré dans la toile en Kg/m.
ø_f : diamètre du filin inséré dans la toile en mm
ø_d :diamètre du câble de drisse en mm
ø_a : diamètre du câble d'anneau en mm
ø_br :diamètre du câble de bras en mm
ø_m :diamètre de pied de mât en mm
K_d : coefficient de sécurité du câble de drisse.
K_br et K_br' : coef de sécurité du câble de bras toile tendue et en début de repliement.
Cu : couple utile sur treuil en Kgf m

Représentation graphique des efforts

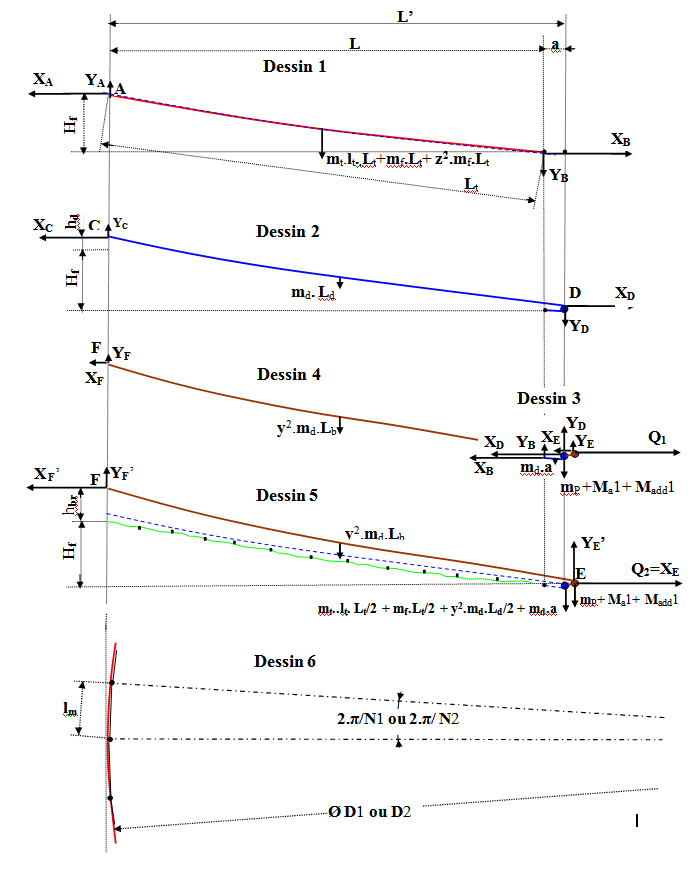
A/ Equilibre d'un filin entre deux rectangles de toile quand le velum est tendu (en rouge)

L'équilibre étudié est celui du dessin ci-dessus, celui d'un filin porteur inséré entre deux rectangles élémentaires de toile. Outre son poids propre il porte deux demi rectangles de toile et la partie du câble de drisse détendue. Ayant une composante nulle les deux ensembles de forces perpendiculaires au plan du dessin, exercés par les rectangles de toile voisins, sont ignorés.

La longueur de la toile est L_t = ( L²+ H_f²)^1/2 et sa largeur l_t est calculée en fonction des dimensions de l'amphithéâtre et du nombre de mâts (voir « Définition des symboles utilisés »). Le câble de drisse et le filin de toile sont constitués avec le même matériau et ont des diamètres dans un rapport z.

Les forces d'équilibre sont des actions horizontales et verticales :

--- des réactions X_A, X_B, Y_A, Y_B aux extrémités.
--- à mi distance de A et B le poids de la toile m_t.l_t.L_t, le poids m_f.L_t du filin entre deux rectangles et le poids z².m_f.L_t du câble de drisse détendu, la tension de la toile étant alors assurée par le filin inséré.

Ecrivons que les sommes des projections des forces sur les traditionnels axes X et Y sont nulles :
(1) X_A - X_B = 0 et (2) Y_B - Y_A + m_t.l_t.L_t+ m_f.L_t.(1+z²) = 0

Ecrivons que la somme des moments des forces par rapport au point B est nulle :
(3) Y_A.L – X_A.H_f - m_t.l_t.L_t.L /2 - m_f.L_t.L.(1+ z²)/2 = 0

L'exigence d'une pente p au point bas B du filin inséré dans la toile s'écrit :
(4) Y_B = p.X_B

Un sesame pour la poursuite des calculs :

Si R est la résistance à la rupture d'un câble de section S et K le coefficient de sécurité souhaité sa tension admissible est :
T = R.S /K

Si L est sa longueur et d sa densité sa masse M est : M = S.L.d
En éliminant S entre ces deux équations il vient : T = R.M /(K.L.d)
soit T = R.m /(K.d) en désignant par m la masse par unité de longueur.
Quand on exprime T en Kgf, R en Kgf/mm², m en Kg/m et d en Kg/dcm³ la dernière formule s'écrit :
T = 10³. R.m /(K.d)
La tension maximale du filin inséré dans la toile est au point A. Elle a pour valeur T_f = (X_A²+Y_A²)^1/2.

On a donc:

(5) X_A²+Y_A² = ((10³. R . m_f)/(K_f .d))²

Le système de 5 équations (1), (2), (3), (4) et (5) procure une équation du second degré à inconnue m_f de la forme :
A.m_f² + B.m_f + C = 0

En posant : G = (10³.R)/(K_f .d) ; Z1 = - ((L.L_t.(1 + z²))/(2.(H_f – p.L)))

Z2 = - ((m_t . l_t .L_t.L)/(2.(H_f – p.L))) ; Z3 = p. Z1 + L_t.(1 + z²) ; Z4 = p. Z2 + m_t.l_t .L_t

On a : A = Z1² + Z3² - G² B = 2.( Z1.Z2 + Z3.Z4) C = Z2² + Z4²

Le déterminant de l'équation du second degré est : ∆ = B² – 4.A.C avec lequel on calcule m_f puis :
X_A =X_B = Z1.m_f + Z2 ; Y_A = Z3.m_f + Z4 ; Y_B = p. X_B

De m_f en Kg on déduit le diamètre Ø_f en mm du filin inséré dans la toile.

Ø_f = ((4.10³.m_f)/(Pi.d))^1/2 et le diamètre du câble de drisse : Ø_d = z . Ø_f

B/ Equilibre du brin supérieur de la drisse :

L'équilibre étudié est celui du dessin 2. Quand le velum est déployé de chaque coté de la poulie le câble de drisse est soumis à la même tension que l'est en B le filin inséré dans la toile, soit (X_B² + Y_B²)^1/2.

h_d étant la hauteur entre le point haut du filin et le haut de la drisse, le dénivelé de celle la est à peu de chose près H_d = (H_f +h_d). Le faible dénivelé supplémentaire induit par la distance a entre anneau central et toile est négligé.

En désignant par L' = (L + a) la longueur de la projection du brin supérieur de la drisse et par L_d la longueur approchée de la drisse telle que : L_d = (L'² + H_d²)^1/2 l'équilibre s'écrit :

(6) Y_D² + X_D² = X_B² + Y_B² (7) Y_D + (m_d .L_d) – Y_C = 0

(8) X_D.H_d -((m_d .L_d.L')/2)– Y_D.L' = 0 (9) X_C - X_D = 0

Le système des quatre équations ci-dessus procure une équation du second degré à inconnue X_D de la forme :
A₁.X_D² + B₁.X_D + C₁ = 0 avec :

A₁ = 1+ (H_d /L)² ; B₁ = -(H_d .m_d .L_d/ L ) ; C₁ = (m_d².L_d²/4) - X_B² -Y_B²

A partir de la racine positive de X_D on calcule :
Y_D = X_D .(H_d /L) –(m_d.L_d /2) puis Y_C = Y_D + m_d.L_d

La tension maximale T_C au point C dans un brin de drisse est T_C = (X_C² + Y_C²)^1/2

Le coefficient de sécurité à la rupture du câble de drisse : K_d =((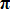. Ø_d²/4). R) /((Y_C² + X_C²)^1/2)

C/ Equilibre de la liaison allant de l'extrémité de la toile à un sommet d'anneau d'araignée situé sur l'arc de plus grand rayon de courbure.

REMARQUE PRELIMINAIRE : la tension de la toile est assurée par les poids de l'anneau central, des poulies et diverses masses additives (pouvant être des pendeloques décoratives) qui y sont attachées.

On convient que lorsque la toile est tendue le bras conserve une tension résiduelle ayant des composantes X_E et Y_E telles que le câble de bras a un diamètre ø_b = y.ø_d

L'équilibre étudié est celui du dessin ci-dessus représentant en coupe la courte liaison entre l'extrémité B de la toile et le sommet E de l'anneau central.

Le point E,sur un arc de plus grande courbure, (voir plus loin dessin vue de dessus) est soumis à un effort centripète horizontal
Q₁ = X_B + (1+ w).X_D qui induit dans le câble d'anneau une tension T_a telle que :

T_a = Q₁/(2.sin(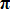/N1)) = (10³.R.m_a)/(K_a .d) d'où m_a = (T_a .K_a .d)/(10³.R)
m_a étant la masse par m du câble d'anneau le diamètre de celui la est : ø_a = ((4.10³.m_a)/(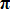.d))^1/2

Sur l'anneau central les bras sont écartés de la1 = (D₁-(2. L')).sin (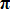/N₁) sur les arcs de grand rayon et de
la2 = (D₂-(2. L')).sin(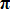/N₂) sur les arcs de petit rayon.

La masse M_a1 d'une longueur la1 de ce câble est M_a1 = (10^-3).((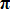.ø_a²)/4).la1.d

La masse M_a2 d'une longueur la2 du même câble est M_a2 = (10^-3).((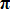.ø_a²)/4).la2.d


Les équations d’équilibre du bras (selon dessin 4 ) lorsque la toile est tendue sont :

(10) XF - w.XD = 0 et (11) XF .(Hf+hbr) + y2.md.Lb.L’/2 -YF .L’ = 0

(12) YF – y2.md.Lb -YE = 0 d’où YE = YF - y2.md.Lb

Elles permettent d’exprimer XF et YF

XF = w.XD YF = ( XF .(Hf+hbr))/L’ ) + y2.md.Lb / 2

La tension maximale du bras est alors Tbr = (XF2 + YF2)1/2

Induisant un coefficient de sécurité Kbr = R /((XF2 + YF2)1/2/((π. y2. ød2)/4))

L’équilibre des forces verticales de la courte liaison entre toile et anneau selon le dessin 3 s’écrit :

YB + YD +YE - mP - Ma1 - Madd1 - md.a = 0
Soit YB + YD + (YF - y2.md.Lb) - mP - Ma1 - Madd1 - md.a = 0
d’ou : Madd1 = YB + YD + (YF - y2.md.Lb) - mP –Ma1 - md.a

Madd2 = YB + YD + (YF - y2.md.Lb) - mP –Ma2 - md.a

D/ Vérification du coefficient de sécurité du Bras au début du repliement

C’est en début de repliement (ou en phase terminale de déploiement) que le bras est le plus tendu. Dans cette configuration le filin inséré et la drisse ne participant plus au portage de l’anneau c’est le bras qui assure seul le portage des divers constituants. Le dessin 5 représente les efforts verticaux en jeu à ces moments la. Les équations d’équilibre sont alors:

(13) Y_E' = m_t.l_t .L'/2 + m_f.L'/2 + (2.m_d.L_d'/2) + m_d.a + m_P+ M_a1 + M_add1

(14) Y_F'- Y_E'- y².m_d.L_b' = 0

(15) (Y_F'.L_d ) – (y².m_d.L_d.L_b'/2) - (X_F'.(H_f+h_br)) = 0

D'où : Y_F'= Y_E'+ y².m_d.L_b' et X_F'= Q₂ = ((Y_F'.L_d) –(y².m_d.L_d.L_b')/2)/(H_f+h_br)

La nouvelle tension du câble d'anneau est alors : T_a'= X_F'/(2.sin(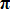/N₁)) induisant un nouveau coefficient de sécurité du câble d'anneau : K_a'= R /(T_a'/(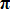.ø_a²/4))

Selon la convention le diamètre de câble de bras est y fois celui de câble de drisse : ø_br = y.ø_d Le nouveau coefficient de sécurité du câble de bras en début de repliement est donc :

K_br' = R /((X_F'² + Y_F'²)^1/2/((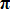. y².ø_d²)/4))

E/ Vérification de l'équilibre d'un sous ensemble du velum (toile tendue)

La somme des masses de tous les câbles, de la toile, de la poulie de drisse et de la masse additionnelle doit avoir la même valeur que la somme des réactions verticales au droit du mât.

Pour un sous ensemble situé sur un arc de plus grande courbure la somme des masses est :
MT1 = (m_t.l_t.L')+(m_f.L')+(y².m_d.L_b')+(2.m_d.L_d')+ M_a1+M_add1+ m_p

Pour un sous ensemble situé sur un arc de plus petite courbure la somme des masses est :
MT2 = (m_t.l_t.L')+(m_f.L')+(y².m_d.L_b')+(2.m_d.L_d')+ M_a2+M_add2 + m_p

La somme des réactions verticales au droit du mât est dans les deux cas : RT = Y_A+Y_C + Y_F

Les calculs numériques assistés par ordinateur indiquent que l'égalité MT1 = MT2 =RT est respectée quelque soient les combinaisons des paramètres d'entrées.

F/ Dimensionnement des mâts, de section circulaire de diamètre øm réalisés avec un bois de résistance à la rupture R_m

Le moment fléchissant maximal appliqué à un mât est en Kgf.mm :
Mf = 10³. X_F'.(H_f +H_br) et I /v = (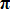 /32).ø_m³

Pour respecter le coefficient de sécurité K_rm souhaité par rapport à la résistance à la rupture R_m du bois utilisé on doit avoir :
R_m/K_rm = Mf/(I /v) = 10³. X_F'.(H_f +h_br)/((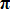 /32).ø_m³)

D'où ø_m = (10³. X_F'.(H_f +h_br).K_rm /(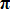 /32). R_m))^1/3

G/ Calculs divers

Longueur totale de l'anneau central : LTa = 2.α.(D₁-2.L) + 2.β.(D₂-2.L)

Masse totale de l’anneau central : MTa = m_a .LTa

Masse totale du velum (toile +câbles + poulie) : MTV = N. MT1 = N. MT2

Masse totale de toile : MTT = N. m_t.l_t.L_t

Surface couverte: Sc = 2.L.(α.D₁+ β.D₂) - (2.L²(α + β))

Masse totale du velum par m2 : M/m2 = MTV/ Sc

Surface totale de toile utile : Su = N. l_t. L_t

Longueur totale de câble pour drisse : LT_d = 3.L_d.N (environ)

NOTA : 3 parce qu'il peut y avoir une longueur L_d stokée sur le tambour de treuil

Longueur totale de câble de bras : LT_b = L_b.N (hors brins morts)

H/ Vérification du câble inférieur de drisse en cours de déploiement ou de repliement. ( voir dessin 5 )

Au cours des manœuvres c'est le brin inférieur de drisse qui porte la toile par l'intermédiaire des anneaux liés à celle la. Dans cette configuration la vérification du câble de drisse doit être opérée avec un calcul « aux éléments finis ». Celui la a été effectué pour le velum en projet sur les arènes du Puy du Fou avec des anneaux espacés de 1,5 m. Il suffit que le brin inférieur de drisse ait un certain mou (d'une valeur très acceptable) pour que les efforts de tous ordres restent inférieurs à ceux de la configuration « toile tendue ».

I/ Puissance et effort de manœuvre utiles

Jusqu'à la phase finale de tension de la toile l'énergie pour le repliement de la toile est, à peu de chose prés, celle de l'élévation de son centre de gravité de la demi valeur du dénivelé, soit Hf/2 . Pour un rectangle élémentaire de toile l'énergie en Kgm est donc : mt.Lt.lt .Hf/2. Si l'opération se fait en quelques minutes il est aisé de voir que la puissance par mât n'est que de l'ordre d'une cinquantaine de watt. C'est dire qu'un seul homme suffit amplement pour assurer la quasi-totalité du repliement. Il est même envisageable que toute la manœuvre, y compris la mise en tension finale puisse se faire avec deux ou trois fois moins d'hommes que de mâts. En fin de tension de la toile l'effort ponctuel maximal à exercer sur le brin supérieur de drisse en C est :

T_dC = (Xc² + Yc²)^1/2

LES EQUATIONS QUI PRECEDENT ONT ETE VALIDES PAR BUREAU VERITAS à fin 2004.

J/ Calculs assistés par ordinateur

Toutes les équations numérotées ci-dessus ont été traduites en écriture informatique. A plus de 70 ans premier exercice du genre pour René Chambon. Il découvrait que le 3,14 de ses 20 ans devait s'écrire (Pi()) ! A partir de valeurs numériques attribuées à une vingtaine de paramètres d'entrées le très commun logiciel Excel donne quasi instantanément tous les efforts en jeu, les diamètres de câbles et leurs coefficients de sécurité, la section des mâts. Il vérifie aussi que toutes les équations d'équilibre utilisées sont bien respectées et que la somme de toutes les masses en jeu (MT) est strictement égale à la somme algébrique des efforts verticaux appliqués sur le mât (RT). Et sur le bâti (dernière colonne de droite).

K/ Applications numériques

La vingtaine d'entrées et les sorties de calculs assistés par ordinateur tiennent sur une seule page A4.

Les deux tableaux qui suivent sont des calculs numériques assistés par ordinateur, pour le Colisée et pour les arènes de Nîmes. Il a été retenu des cordes en chanvre avec une résistance à la rupture de 8,8 Kgf/mm² et une densité de 0,9 Kgf/dcm³, des valeurs relevées dans le catalogue du fabricant CORDALPES. La toile est en lin d'un poids réaliste de 0,3 Kg/m² comme, sans doute, celle des toges des belles romaines de jadis. Les résultats montrent on ne peut plus clairement qu'il y a près de deux mille ans les romains pouvaient équiper de velums les deux amphithéâtres, avec des cordes de diamètres très ordinaires, de 10 à 60 mm. Cela avec des coefficients de sécurité de 6 on ne peut plus sécurisants. Le poids des couvertures ressort à moins d'un kilo par m2 : stupéfiant !

La pente p du filin inséré dans la toile a été choisie à 5%. Une valeur plus faible réduirait sensiblement les masses de l'anneau central et des masses additives (pendeloques).

Pour bien protéger les premiers rangs de notables des rayons obliques du soleil le dit anneau devait être placé assez bas : tant mieux pour réduire les diamètres des cordes et les efforts! Il a été arbitrairement retenu un dénivelé de 14 m pour le Colisée et de 10 m pour les arènes de Nîmes.

Les calculs présentés prennent en compte des anneaux centraux réalisés avec des cordes en chanvre travaillant avec un coefficient à la rupture de 6. Il est vraisemblable que les Romains réalisaient l'anneau central avec une chaîne en fer beaucoup plus résistante que nécessaire : masses additives (pendeloques) plus légères, coefficient de sécurité élevé, insensibilité à l'hygrométrie, facilité de fixation des poulies de drisses et des bras.